

Some things to note about such lambda expressions: When we discussed combinators in JavaScript, we gave this function a name. Here is a simple Lambda Abstraction of a function: It is worth looking at this notation before studying haskell-like languages because it was the inspiration for Haskell syntax. Lambda Calculus expressions are written with a standard system of notation. The operations we can apply to Lambda Calculus expressions to simplify (or reduce) them, or to prove equivalence, can also be applied to pure functions in a programming language that supports higher-order functions.

The Lambda Calculus is also important to study as it is the basis of functional programming.
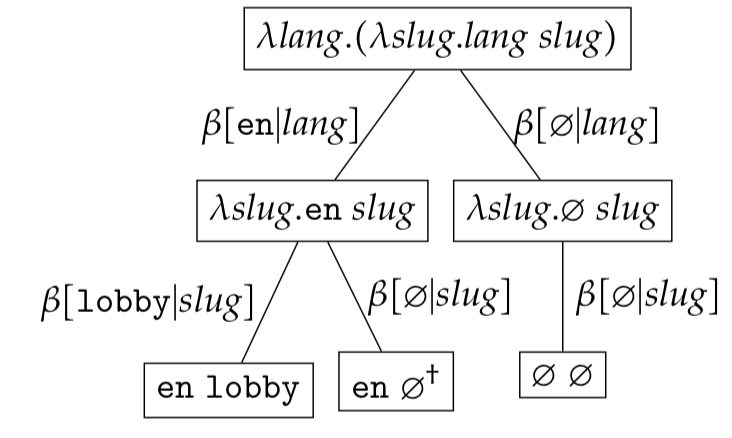
It has been proven that, as a model of computation, the Lambda Calculus is just as powerful as Turing Machines, that is, any computation that can be modelled with a Turing Machine can also be modeled with the Lambda Calculus. However, while the Turing Machine is based on a hypothetical physical machine (involving tapes from which instructions are read and written) the Lambda Calculus was conceived as a set of rules and operations for function abstraction and application. You are probably aware of the more famous model for computation developed around the same time by Alan Turing: the Turing Machine. The Lambda Calculus is a model of computation developed in the 1930s by the mathematician Alonzo Church.


 0 kommentar(er)
0 kommentar(er)
